Highlight
Stochastic Simulations of the ErbB Signaling Pathways Demonstrate the Importance of Spatial Organization in Signal Transduction
Achievement/Results
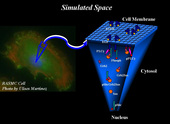
Overexpression of the ErbB family of receptors often leads to an activation of intracellular signaling pathways that are responsible for controlling cellular proliferation, growth, differentiation, and apoptosis. Therefore, overexpression of the ErbB receptors is often associated with many different cancers, and extensive efforts have been made to understand the signaling events due to ErbB activation by developing complex computational models. Although models have grown in complexity, little work has been done to uncover the spatial-temporal dynamics of receptor interactions and how it affects downstream signaling within this pathway. Under the guidance of her mentor Prof. Jeremy Edwards and co-mentor Prof. Bridget Wilson at the University of New Mexico, Michelle Costa, a Trainee supported by the NSF IGERT program on Integrating Nanotechnology with Cell Biology and Neuroscience, has developed a coupled spatial-nonspatial simulation algorithm, CSNSA, which couples a spatial stochastic model of receptor reaction and diffusion on the cell membrane with a nonspatial stochastic model of intercellular reactions and interactions in the cytosol, as illustrated in Fig 1. Using this framework, the effects of downstream signaling due to receptor clustering and spatial heterogeneity on the membrane have been elucidated. The ErbB family of receptors under normal physiological conditions regulates key cellular processes, such as growth, proliferation, and differentiation. Overexpression of these receptors deregulates normal cellular function and can be a contributing factor to tumorgenesis. There are four members of ErbB family: ErbB1, ErbB2, ErbB3, and ErbB4, and each family member has its own unique ligand specificity, kinase activity, and spatial organization on the membrane. ErbB1, which is the focus of Michelle Costa’s studies, is also known as EGFR (epidermal growth factor receptor), and EGFR activation induces the mitogen-activated protein kinase (MAPK). Ligand binding to the EGFR fixes it in the open conformation, which enables it to dimerize and transautophosphorylate itself. Once phosphorylated, many cytosolic proteins such as Grb2, Sos, and Shc, are recruited to the membrane, where they bind to the phosphorylated receptor, thus forming signaling scaffolds. This establishes the membrane as the main platform for cell signaling events. Due to the importance of this pathway, mathematical models have been developed to gain a better understanding of this system. The most popular method for modeling this pathway is with ordinary differential equations (ODEs), which provide a temporal profile of species concentrations. Over the past decade, ODE models of this system have evolved in complexity, becoming both larger and having more experimentally constrained parameters. The first EGFR model was introduced in 1996 and had 35 reactions, whereas the most complete models available today contain hundreds of reactions. In spite of this growth in the number of reactions and complexity, the question remains whether modeling signaling pathways using ODEs is capable of capturing the true nature of the system, because ODE-based models assume that the system is well mixed. Experimental evidence has proven that the well-mixed assumption may not be accurate for the EGFR system, where significant spatial heterogeneity has been shown to occur. Spatial modeling includes partial differential equations (PDEs), agent based modeling, and spatial Monte Carlo (MC) methods. Among these different types, spatial MC methods have emerged as a powerful numerical molecular simulation tool for studying membrane dynamics. In earlier work by Prof. Edwards’ group, spatial MC methods have been implemented to study ErbB reaction and diffusion and to understand signal propagation due to these reaction and diffusion events. Building on that work, Michelle Costa has developed a new computational framework that merges a spatial kinetic Monte Carlo, SKMC, for modeling reaction and diffusion events on the membrane with a stochastic simulator algorithm, (SSA) for modeling cytosolic interactions. The new algorithm can be used to determine the effects that receptor clustering has on signal propagation. To test the effects of clustering, three different domains are defined, as shown in Fig. 2: a high receptor density domain with 705 receptors per mm2 (shown in the blue), a dispersed domain with 106 receptors per mm2 (shown in magenta), and a clustered domain which initially contains 705 receptors per mm2 and is then allowed to diffuse to 106 receptors per mm2 (shown in cyan). In Fig. 3, the CSNSA simulation (magenta, cyan, and blue) is compared the with the ODE model (purple and red). The most notable differences occur in the clustered domain (cyan), which had the same receptor concentration of 75nM as the non-clustered domain (magenta), but was initially confined to a smaller region. The clustered domain showed a significant increase in the amplitude of signal propagation in comparison to the ODE solution. These results illustrate how spatial heterogeneity increases the amount of signal propagation downstream.
Address Goals
Cancer is a disease which kills hundreds of thousands of Americans per year, making cancer research a hallmark in health care. Within the past decade, there has been a paradigmatic shift in cancer treatment, moving from therapies that destroy all cells to therapies that target specific mutated proteins within the oncogenic cells. This revolution in cancer therapy became possible as a result of improved understanding of the signaling pathways involved in oncogenesis. In particular, therapies are being developed to target oncogenes such as ErbB1 and ErbB2, and facilitate tumor suppressors such as p53. ErbB receptors are also being used to target drug delivery vehicles in order to make therapies cancer-specific. The success of all of these applications in cancer therapy relies upon a fundamental understanding of spatial-temporal protein interactions, which will advance the frontiers of cancer research leading to better quality of life. Although much of science is based on a reductionist approach, systems biology incorporates an integration approach to understand interactions of systems. Cancer is a primary example of how reductionism can fail. Cancer can involve hundreds of mutations, which enable it to proliferate, evade apoptosis, become insensitive to anti-growth signals and self-sufficient on growth signals, sustain angiogenesis, and to metastasize and invade other tissues. This is why it is necessary to take into account the intricate signaling pathways that contribute to the disease and their spatial domains. Such details can be modeled in silico to test multiple hypotheses to elucidate mechanism, drug candidates, and to develop combinatorial drug treatment therapies. Using computational power to understand these mechanisms will propel cancer research into the twenty-first century and make the nation a global leader in science and engineering. This project fosters the secondary strategic NSF goal of learning. Computational modeling of biological pathways encompasses multiple disciplines, ranging from mathematics, physics, chemistry, and computer science, to cell biology, molecular biology, genetics, and physiology. Bringing together these vast disciplines fosters appreciation, team work, and interdisciplinary skills which all contribute to development of world-class workforce well prepared for the challenges of the 21st century.